教養学部報
第535号 ![]()
物理は楽しい――遊び心でノーベル賞――
吉岡大二郎
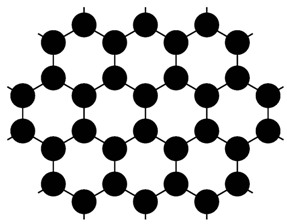
grapheneの結晶構造。
丸は炭素原子、線は共有結合を表す。カエルを磁場の力で空中浮揚させた功績で二〇〇〇年度のイグ・ノーベル賞に輝き、ヤモリの足の粘着力を研究して強力な粘着テープを作ったガイム博士が、今年度はノボセロフ博士と共にノーベル物理学賞を受賞した。受賞理由は二次元の結晶を同定して、測定を行い、この物質が物理学の対象として興味深く、実用面でも大いなる可能性を秘めていることを明らかにしたというものである。しかし、最も注目に値するのは二次元結晶実現に用いられたローテクでユニークな方法かも知れない。
彼らが対象とした2次元物質とは図のように炭素原子が六角格子を組んだものである。化学でおなじみのベンゼンを直線的につなげると、ナフタレン、アントラセン、テトラセン、……というアセンの系列ができるが、これを平面的に拡げて水素を取り去ったものと考えても良いし、鉛筆の芯に含まれている黒鉛(グラファイト)を薄くしていった極限の物質といっても良い。そう、グラファイトとは、この六角格子が積み重なってできているものなのだ。
この二次元結晶はgrapheneと名付けられ、グラフィーンと発音されるが、日本では奇妙なことにグラフェンという書き方が定着している。(変な言葉は使いたくないので、以下ではグラフィーンを用いる。ちなみに、グラフィーンの各炭素に水素を結合させたものはgraphaneである。どのように発音するかは読者の想像に任せる。)
さて、このグラフィーン、実は世界中で何十億もの人々が大昔から日夜生産してきたかも知れない。ほら、君が鉛筆で書いた文字の中に隠れているではないか。しかし、そこいらじゅうにあるかも知れないけど、ちゃんと見つけて、厚さや電気抵抗の測定をして見せて初めて二次元結晶を見つけたと言えるのだ。
ガイムとノボセロフは鉛筆の筆跡の中に見つけたのだろうか? そうではない、筆跡中では無数の結晶が重なり合い、粘土なども混ざっている。一枚だけを取り出さなければだめなのだ。そのために彼らが用いたのがスコッチテープである。グラファイトの単結晶を薄くして行けば最終的にグラフィーンが得られる。グラファイトの両面にスコッチテープを貼り付けて引き剥がすと、グラファイトは二つに剥がれる。これをくり返せば、グラファイトは薄くなって行くわけだ。
1mmの厚さのグラファイトはほぼ三百万層のグラフィーンが積み重なってできている。これはすごい数だが、毎回厚さが半分になるとすれば、なんと、たったの二十回程度で、一原子の厚さの二次元結晶が得られるのである。こんな事ができるのは、グラフィーンが非常に強い物質であることと、グラファイトはグラフィーンがテープの粘着力より弱い引力で積み重なってできていて、容易に劈開することによっている。鉛筆として使えるのも容易に劈開するからである。
鼻歌混じりでテープを合わせたり、剥がしたりして遊んでいると、グラフィーンがテープ上にできあがる。原子一個の厚さしかないからほとんど透明である。これを平らな石英の上に転写して、グラフィーンを見つけるのが次の仕事だ。ここで使うのは普通の光学顕微鏡である。今、ほとんど透明と言ったが、実は光をほんの少し吸収するので、原子一層の物質が見えるのだ。大きな結晶なら肉眼でも見えるだろう。光を吸収するのは後で述べるグラフィーンの特殊な電子状態の結果である。なお、吸収率には重要な物理定数が顔を出す。素電荷、光速度、プランク定数、真空の誘電率を組み合わせて無次元の微細構造定数が作られ、ほぼ一三七分の一という値を持つ。これをπ倍すると、0.023になる。この分だけ光が吸収されることが理論的に示され、実際、この通りの吸収をすることで、見えるのであった。
このようにグラフィーンを見つけて何が画期的だったのだろうか。第一は本当に一原子の厚さの二次元結晶が存在できたという事だ。簡単にちぎれたり、原子がバラバラになったり、丸まったりしないで存在することが実証できた。(因みに筒状に丸まるとカーボンナノチューブというものになり、発見者の飯島氏はついこの間までノーベル物理学賞の有力候補であった!)グラフィーンは厚さ当たりではどんな物質より強く、弾力もあり、如何に小さな原子でも通過できない網であることが明らかにされている。
画期的なことの二番目は電子状態である。この物質の電子状態が非常に興味深いものであることは理論的には半世紀も前から知られていた。普通の金属や半導体中の電子は速度に比例した運動量を持ち、運動エネルギーはニュートン力学と同じで運動量の自乗に比例する。このような電子はシュレーディンガー方程式(原子の世界の法則である量子力学の基本方程式)で記述される。
ところで、物体の速度が光速度に近づくとニュートン力学ではだめで、アインシュタインの相対性理論が必要になることは良く知られている。高速の物体では運動量と速度は比例せず、エネルギーはほぼ運動量に比例するようになる。このような状況を量子力学で記述するのがディラック方程式である。グラフィーンが面白いのは、電子のエネルギーが運動量に比例し、質量をゼロにしたときのディラック方程式で記述できることである。
グラフィーン中では如何なる運動量の電子でも全て同じ速さ(光速の三〇〇分の一程度)で走っているのだ。もちろんこんな事は半世紀前から分かっていた。しかし、実際にグラフィーンを実現して、この奇妙な振る舞いの電子達と遊ぶことはできなかったのだ。
今、世界中で物理学者達が喜々として、この電子達に光を当てたり、電場をかけたり、磁場をかけたりして遊んでいる。電子は集団にした方がおもしろい振る舞いを見せてくれるが、グラフィーンでは電子の密度は簡単に変えることができ、負にすることもできる。(負の密度とは半導体の言葉では正孔をたくさん作ることだし、ディラック理論では陽電子を好きなだけ作れる事に対応する。)この結果、理論による予測が次々と実験で確かめられている。光の吸収が微細構造定数で決まることも確かめられたし、二次元系に特有の量子ホール効果が起こり、ホール抵抗が素電荷とプランク定数のみで決まることも確かめられた。この他にも様々な発見があり、毎年二千篇以上の論文として発表されている。
グラフィーン(やカーボンナノチューブ)については「新しい物理がない」とノーベル財団を批判する人がいる。しかし、ノーベル賞はグラフィーンがもらったのではない。コロンブスの卵的発想で、物理の新しい大きな遊び場、未知の宝物が埋まっているかも知れない遊び場を作ったガイムとノボセロフが授賞したのである。
(相関基礎科学系/物理)
無断での転載、転用、複写を禁じます。

