News
Topics October 8, 2024
[Research News]Decomposing Thermodynamic Dissipation of Linear Langevin Systems via Oscillatory Modes and Its Application to Neural Dynamics――Toward a Thermodynamic Understanding of Neural Dynamics――
October 8th, 2024
The University of Tokyo
Points
- A novel theoretical relation linking thermodynamic dissipation (entropy production rate) and oscillatory phenomena was discovered.
- Using the relation derived in this study, we have shown that the origin of the entropy production rate in brain activity differs between awake and anesthetized states.
- Our results may lead to a better understanding of oscillatory phenomena widely observed in various living systems, including the brain, from the perspective of non-equilibrium thermodynamics.
Summary
Daiki Sekizawa, a graduate student at the Graduate School of Arts and Sciences, University of Tokyo, Sosuke Ito, an associate professor at the Graduate School of Science, University of Tokyo, and Masafumi Oizumi, an associate professor at the Graduate School of Arts and Sciences, University of Tokyo, have shown that one term of the thermodynamic dissipation (Note 1) can be decomposed into contributions for each oscillatory mode. By applying the decomposition to open ECoG data (Note 2) of monkey brain activity, they found that most of the thermodynamic dissipation in the anesthetized state comes from delta waves (Note 3), which are slow oscillations, while in the resting state, brain wave components such as theta waves and alpha waves, which are faster oscillations than delta waves, contribute more. These results may be useful for understanding oscillatory phenomena that are universally observed in various living systems, including the brain, from the point of view of non-equilibrium thermodynamics.
Contents
In non-equilibrium thermodynamics, the relations between the entropy generation rate (thermodynamic dissipation), and information processing have been studied. This theoretical development has led to the application of non-equilibrium thermodynamics to the understanding of information processing in various living systems, including the brain, which is the target of our research.
On the other hand, oscillatory phenomena are often observed in various living systems. In the dynamics of neural activity in the brain, oscillatory phenomena such as alpha and delta waves have long been the focus of attention. However, the relationship between the entropy production rate and oscillation has yet been unknown. In this study, we derived a novel relation between oscillation and entropy production rate. By applying the equation to actual neural data, we quantified how brain wave components with different frequencies, such as alpha waves and delta waves, contribute to the entropy production rate.
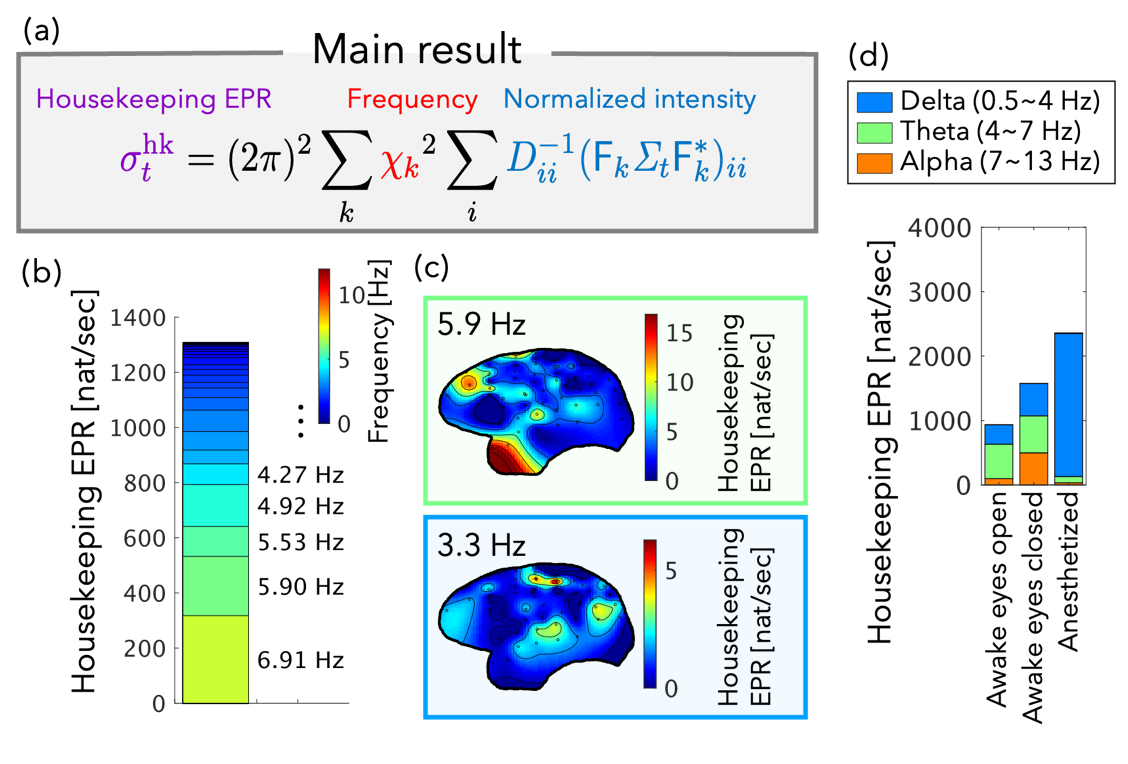
Specifically, we have shown that in the linear Langevin system (Note 4), one term of the entropy production rate, the housekeeping entropy production rate, can be decomposed into the contribution of each oscillatory mode (Fig. (a) and (b)). According to our decomposition, the contribution of each oscillatory mode to the entropy production rate is determined by the product of the square of the frequency and the oscillatory intensity. In other words, the higher the frequency or the stronger the intensity of the oscillatory mode, the greater the contribution to the entropy production rate. When the noise on the system is independent for each dimension, we can also know the magnitude of the contribution that each dimension has. This means that when analyzing brain activity data, the contribution of each electrode for each oscillatory mode can be known (Fig. (c)).
We applied this decomposition to monkey brain activity data (Neurotycho (Note 5)) to investigate how brain wave components such as alpha and delta waves contribute to the entropy production rate. We found that in the anesthetized state, most of the entropy production rate comes from delta waves, which are slow oscillations, while in the resting state, brain wave components such as theta and alpha waves, which are faster oscillations than delta waves, also contribute about half of the total (Fig. (d)).
Our method may lead to an understanding of oscillatory phenomena commonly observed in the dynamics of living systems from the perspective of nonequilibrium thermodynamics. In addition, given the relations between the entropy production rate and information processing in non-equilibrium thermodynamics, our decomposition may lead to an understanding of how brain wave components such as alpha and delta waves can affect information processing in the brain as they change depending on the brain state.
Researcher Information
The University of Tokyo
Department of General Systems Studies
Daiki Sekizawa, Graduate student / JSPS Research Fellow
Masafumi Oizumi, Associate professor
Department of Physics / Universal Biology Institute
Sosuke Ito, Associate professor
Paper Information
Journal:Physical Review X
Title:Decomposing Thermodynamic Dissipation of Linear Langevin Systems via Oscillatory Modes and Its Application to Neural Dynamics
Authors:Daiki Sekizawa, Sosuke Ito, Masafumi Oizumi*
DOI:10.1103/PhysRevX.14.041003
URL:https://link.aps.org/doi/10.1103/PhysRevX.14.041003
Acknowledgements
This work was supported by JPSP KAKENHI (23KJ0799, 19H05796, 21H01560, 22H01141, 23H00467, 24H00834, 20H05712 and 23H04834), JST Moon Shot Type R&D Project (JPMJMS2012), JST ERATO (JPMJER2302), JST CREST (JPMJCR1864), and UTEC-UTokyo FSI Research Grant Program.
Glossary
(Note 1) Thermodynamic dissipation (entropy production rate).
A quantity that expresses the irreversibility of a physical process.
(Note 2) ECoG (electrocorticography)
A type of recording method of brain activity that records brain electrical signals from electrodes placed on the surface of the brain.
(Note 3) Brain wave components such as theta waves and alpha waves
Brain waves often exhibit characteristic oscillatory phenomena. Among them, those between about 0.5 to 4 Hz are called delta waves, those between 4 and 7 Hz are called theta waves, and those between 7 and 13 Hz are called alpha waves.
(Note 4) Linear Langevin system
A linear dynamical system subject to stochastic external forces, in which the time evolution of the state vector x is written as dx=DAxdt+√2D dB, where A is a matrix, D is a positive definite symmetric matrix and dB is the standard Brownian motion.
(Note 5) Neurotycho
A public dataset of monkey ECoG containing brain activity recorded in awake and anesthetized states.
―Public Relations Office, Arts and Sciences, University of Tokyo―
