教養学部報
第657号 ![]()
貴重な資源である量子コヒーレンスが、いくらでも増幅できることを理論的に解明
白石直人・髙木隆司
量子コヒーレンスは、異なる量子状態の量子的な重ね合わせのことで、これは量子力学の一つの顕著な特徴です。量子コンピュータや量子通信など、近年その技術発展が著しい量子情報処理においては、多くの量子コヒーレンスが必要となります。しかし、量子コヒーレンスを伴う状態に対する量子操作には、原理的な制限が存在することが知られています。特に、我々の住む世界ではエネルギー保存則が成り立っていますので、エネルギー保存則を満たす操作しかできないという条件の下で、どのような状態の変換ができるかを考えるのは自然な問題設定です。以降、この解説で行う「操作」はすべてエネルギー保存則を満たす操作とします。
この設定で考えると、もし外から何も助けを借りない場合には、エネルギー固有状態(エネルギーの値が定まっている状態)間の量子コヒーレンスは減る一方で、量子コヒーレンスを増やすことはできない、ということが簡単に分かります(図左)。このことは、状態変換の立場から見ると「量子コヒーレンスについての制約は可能な状態変換を厳しく制限している」こと、量子コヒーレンスの立場から見ると「量子コヒーレンスは貴重なリソース(資源)である」ことを示唆しています。このような、「どのような状態変換が可能か」という問題や、「そもそも各状態が持つ『貴重なリソース』をどのように定量化するか」という問題は、量子情報理論の一分野である量子リソース理論という研究領域で活発に研究されています。
量子リソース理論では、より幅広い状態変換を実現させるために、「触媒」と呼ばれる外部の補助系を利用する方法がよく用いられます。触媒という名前は化学反応とのアナロジーで付けられたもので、その補助系自身の状態は操作の前後で一切変化しないけれども、操作対象の系の状態変換を助けてあげるような、そうした補助系を「触媒系」と呼びます(図右)。我々は特に、着目系と触媒系の間に微小な相関は生じていてもいい、という「相関した触媒」の設定を用いることにします。量子リソース理論のこれまでの研究では、多くの場合には、相関した触媒を用いると、状態の変換能力が向上するという結果が得られていました。特に、微小な量子系特有の「些末な」制限がなくなり、物理的に有意味な制限だけが残る、という振る舞いが観察されていました。しかし量子コヒーレンスについての制約の場合には、相関した触媒を用いても、もし始状態が一切量子コヒーレンスを持っていない場合には、変換後の状態も相変わらず量子コヒーレンスを持つことができない、という禁止定理が先行研究で得られていました。つまり、量子コヒーレンスに関する変換については、この場合には、相関した触媒は一切状態変換の能力を向上させなかった、ということです。
そこで我々は、一般の始状態に対して、相関した触媒を用いた操作で、量子コヒーレンスを持つ状態がどのように変換可能かを調べました。すると驚くべきことに、もし始状態が適切なモード(二つのエネルギーの組)にわずかでも量子コヒーレンスを持つのであれば、そのモードのコヒーレンスを好きなだけ増幅することができ、その状態を任意の状態に変換できるということが分かりました(図右)。つまり、相関した触媒の助けを借りれば、「わずかだが非ゼロの量子コヒーレンス」が「いくらでも大きな量子コヒーレンス」になるという変換が実現できるというわけです。これは量子コヒーレンスについての先行研究で示唆されていたのとは真逆の結果で、相関した触媒の助けのもとでは、量子コヒーレンスは状態変換においてほとんど何の障壁にもならない、ということを意味しています。
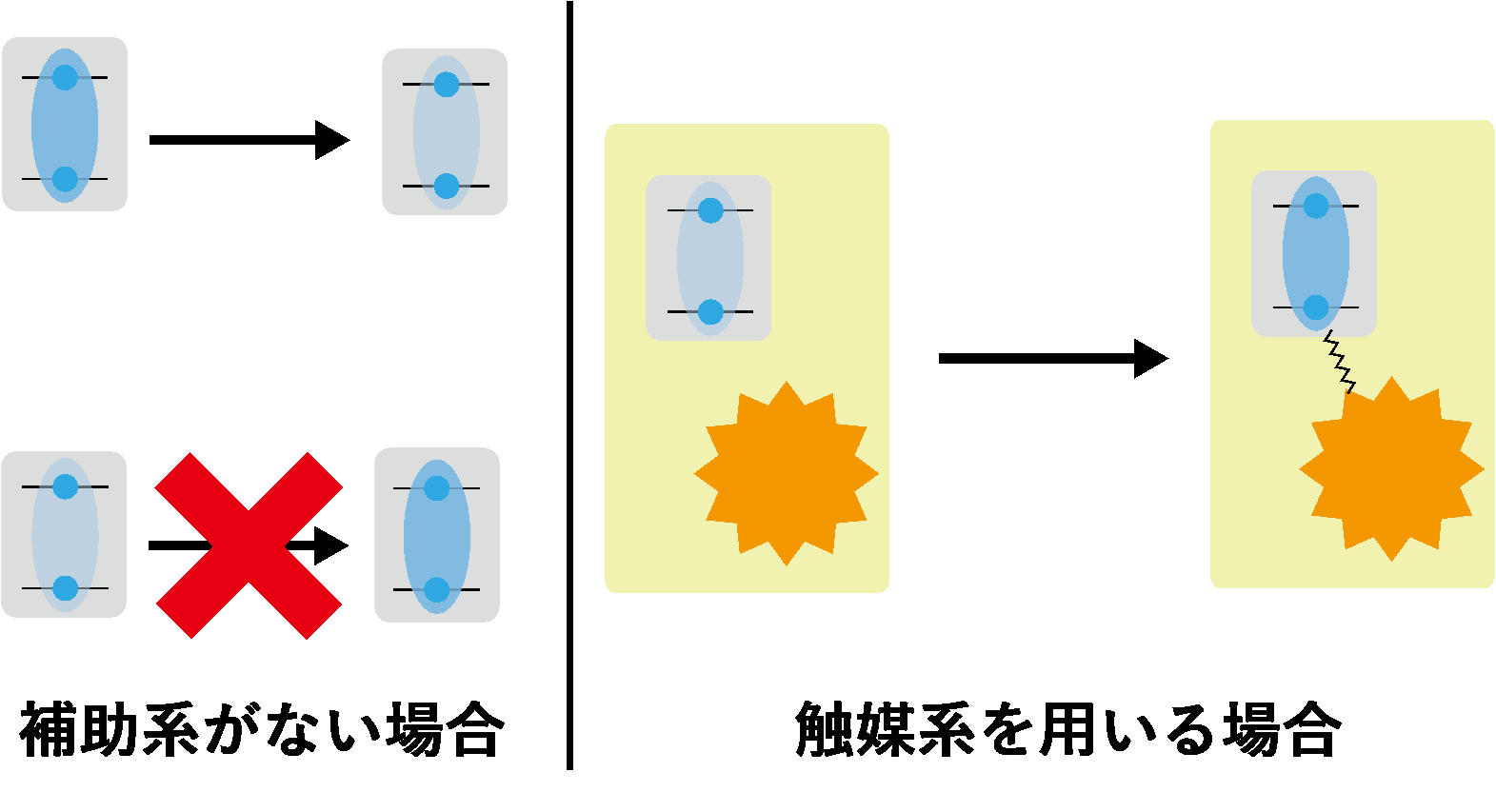
(右)触媒系という補助系を用いる設定。この場合、量子コヒーレンスの増幅が可能である。
我々はさらに、先行研究の結果を改良し、たとえ始状態が量子コヒーレンスを持っていたとしても、適切なモードの上に量子コヒーレンスがない場合には、相関した触媒の助けを借りても、相変わらずそのモード上に量子コヒーレンスを生み出すことはできないことも明らかにしました。これらの結果を組み合わせることで、量子コヒーレンスの変換は、「多い/少ない」という量的な関係ではなく「非ゼロ/完全にゼロ」という境界こそが重要であり、コヒーレンスが存在しさえすればその量は変換可能性には影響しないことが分かりました。この結果は、これまでの量子リソース理論で得られていた結果とは質的に異なるタイプの結果であり、理論的にも極めて興味深いものであるとともに、今後の量子情報処理デバイスを考案するうえで、量子コヒーレンスによる制限がどのように乗り越えられるかについての方向性を指し示すものでもあります。
(相関基礎科学/物理)
〇関連情報
【研究成果】貴重なリソースである量子コヒーレンスが 無制限に増幅可能であることを理論的に解明
https://www.c.u-tokyo.ac.jp/info/news/topics/20240513140000.html
無断での転載、転用、複写を禁じます。

