教養学部報
第660号 ![]()
ねじると大きくなる自己集合体
阿部 司・平岡秀一
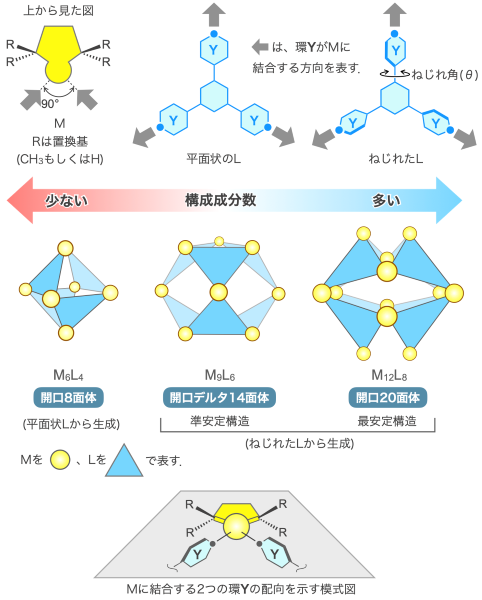
分子が自発的に集まり、秩序だった構造を形成する現象を分子自己集合と言い、自然界に遍在し、材料の作製にもこの現象を利用しているものがあります。自己集合体を構成する分子は様々ですが、その中に金属イオンや金属錯体(M)と配位子(L)と呼ばれる分子の二種類の間を結ぶ配位結合という可逆な結合を介して、集合体MaLb(a、bはMとLの成分数を表す)を形成する系があります。ある化学平衡A ⇄ Bの自由エネルギー変化(ΔG)はΔG=ΔH−TΔS (式1)(ΔHはエンタルピー変化、ΔSはエントロピー変化、Tは絶対温度)で表され、ΔGが負で絶対値が大きい程平衡がBに偏ります。自己集合では、AはMとLがバラバラの状態に、BはMaLbに相当します。あるMは二つのLと結合し、Lを互いに約90度で配置できます。一方、LにMと結合できる部位が三つ存在する場合、MとLそれぞれの結合部位を全て結合させると、M3nL2n(n=1, 2, 3, ··) が得られます。毎年、ノーベル化学賞の有力候補者として名前が挙がる本学の藤田誠卓越教授は一九九六年に図に模式的に示す平面状のLとMからM6L4開口八面体(正八面体から互いに辺を共有しない四つの面を取り除いた構造)を形成することを発見しました。一般的に、成分数が多い集合体の形成は(式1)のΔSが負で絶対値が大きくなり不利なため、成分数が多く大きな構造体をいかに形成するか、という問題があります。MaLb集合体の形成でこれを解決する主な戦略は、Lの結合部位の方向を変えることで、成分数が少ない集合体を歪ませ、ΔHを大きくすることでした。例えば、平面状のLからM3L2を形成すると歪みが大きい一方、M6L4では歪みが小さく、エントロピーの不利を乗り越えてM6L4を形成したと説明できます。
ここで、Lの中の三つの六員環(Y)をねじった配位子を考えます。これまでの知見に基づくと、環YをねじってもMと結合する部位の方向は変化しないため、M6L4開口八面体が生成すると考えられてきました。ところが、実際にねじった配位子を作って調べると、M12L8開口二十面体が最安定構造として生成することが分かりました。これは意外ですが、(式1)に従って説明できるはずです。そうなると、M12L8はΔSの大きな不利があるにもかかわらず、M6L4に比べそれを乗り越えるだけのΔHの利得があることになります。これを確認するために、M6L4とM12L8の中に見られる環状構造(開口部を取り巻く環構造)に着目し、これらの歪みとねじれ角(θ)の関係を幾何学的に調べました。幾何学解析では、大学院生の竹内啓介さん(統合自然科学科 物質基礎科学コース卒業生)が学部四年生の時のスポーツ科学の講義で学んだ身体の関節の動きを幾何学的に表現する知識を使って、歪みを数値化するプログラムを作成し解析を行いました。その結果、ねじった配位子のねじれ角である38度付近でM12L8を構成する四員環構造の歪みはゼロに近く、一方M6L4を構成する三員環構造ではθが大きくなるにつれて歪みが大きくなることが分かりました。また、ねじれ角が変化すると、環構造の歪みが変化する理由については、M自体にその謎が隠されていることが分かりました。Mの化学構造を見ると(一番下の図を参照)、Mにある五員環に導入された四つの置換基(R=CH3基)が立体的に嵩高く、Lの環Yがこの五員環に対して90度をなすように制約を受けます。その結果、Mに結合した二つのLの相対的な空間配置が規定されます。このため、Mに結合した二つのLの間には直接的な相互作用は存在しませんが、Mを介して遠隔で幾何学的な相互作用が発生するのです。事実、五員環の置換基(R)を水素にして嵩高さを抑えると、遠隔の相互作用が弱まりM6L4が生成しました。したがって、Lのねじれ角の変化がMを介した遠隔の幾何学的相互作用により構造体全体に伝播することで、自己集合体の構成成分数を増加させる新しい設計戦略が明らかになりました。
この研究では、同じねじった配位子からM9L6開口デルタ十四面体という新しい構造もほぼ100%の収率で生成することを発見しました。同様に環構造の歪み解析を行うと、M9L6はM12L8より歪みが大きいですが、M6L4よりは歪みが小さいため、準安定種として生成したのです。MとLの結合は可逆なため、自己集合体の形成は本質的に化学平衡(熱力学支配)だと考えられてきました。一方、M9L6のような準安定種が100%で生成することを化学平衡(熱力学)で説明できず、速度論支配の帰結であることを示しています。自己集合は多数の可逆な反応からなるネットワーク構造と捉えることができ、可逆な反応ネットワークの中で、準安定なM9L6のみを速度論的に与える経路選択の原理とは何か?という新たな疑問が現れました。我々はすでに、自己集合機構を実験および数理解析によって調べる手法を開発しており、M9L6の形成機構の解明を通して、可逆性と非可逆性という一見相反する現象の境界とも言える状況で起こる問題に対する答えを解き明かしたいと考えています。
(相関基礎科学/化学)
〇関連情報
【研究成果】多座配位子内の二面角変化に基づく構成成分数の多い自己集合体の形成――大きな構造体形成の一般原理――
https://www.c.u-tokyo.ac.jp/info/news/topics/20240909180000.html
無断での転載、転用、複写を禁じます。

