ニュース
![]() 2023.01.12
2023.01.12
【研究成果】脳の状態を制御する際に必要な「コスト」を定量化する新しい手法を提案
東京大学
株式会社アラヤ
発表者
神谷 俊輔(東京大学 大学院総合文化研究科 広域科学専攻 博士課程)
笹井 俊太朗(株式会社アラヤ 取締役CRO兼 研究開発部部長)
大泉 匡史(東京大学 大学院総合文化研究科 広域科学専攻 准教授)
発表のポイント
- 脳がある状態から別の状態に移り変わるのに必要な制御のコストを定量化し、最も効率的な制御入力を求める方法を提案した。提案手法を、人間が様々な認知タスクを行っている最中のfMRIデータに適用し、脳状態の制御に貢献する脳領野を同定した。
- 本研究での制御コスト定量化法は、従来の方法では無視されていた脳活動のノイズの影響を考慮に入れて制御コストを評価できる初めての手法である。
- 脳がある状態から別の状態に移り変わる際の制御コストを定量化することで、様々な認知タスクが人間にどれくらいの負荷を与えるか、精神的疲労などを定量的に評価することができるようになる可能性がある。
発表概要
東京大学大学院総合文化研究科の神谷俊輔 大学院生、大泉匡史 准教授、株式会社アラヤの笹井俊太朗 取締役CRO兼研究開発部部長らは、脳活動の状態遷移を制御する際に必要な制御コストを定量化する新たな数理的手法を提案しました。 私たちは日々、多種多様な認知や行動を行うことができます。なぜ脳は様々な認知や行動を実現することが可能なのでしょうか?この問いを脳の「制御」という観点から解釈すると、脳は自らの状態を適切に制御して、様々な状態に切り替えることが可能であるからと言えます。ある状態から別の状態への状態遷移の制御にどの程度の「コスト」が必要かを定量化すること、あるいは、状態遷移の制御に重要な役割を果たす脳部位を同定することは、脳がどのように認知や行動を実現しているかを理解する上で重要と考えられます。 これまでも、脳の状態遷移の制御コストを定量化する研究はありましたが、脳活動はノイズ(注1)を含み確率的な振る舞いをする事実を考えていなかったことが問題でした。本研究では、脳活動の確率的な振る舞いを考慮して制御コストを定量化する、新たな手法を提案しました。提案手法を、人間が様々な認知タスクを行っている最中のfMRI(注2)データに適用し、脳状態の制御に貢献する脳領野を同定しました。 「脳がある状態から別の状態に移り変わる制御の難しさ」を定量化する本研究を足がかりに、今後、人間が様々な認知タスクを実行する上での負荷や精神的疲労、あるいは精神病など、一見全く異なる現象に、制御という統一的観点から新しい理解を与える可能性があります。また本研究は、脳に外部入力を与えることで、ある目的の状態に遷移させることを目指す研究にも理論的な基盤を与えるものです。 本研究成果は、2023年1月11日に米国科学誌「The Journal of Neuroscience」に掲載されました。
発表内容
[研究の背景]
私たちの脳は非常に複雑な動的ネットワークで、様々な状態に柔軟に遷移して多種多様な機能を実行しています。この点から、脳は必要とする機能、目的に応じて、内部状態(脳活動のパターン)を望ましい状態に遷移させる制御システムと考えることができます。神経ネットワークの特性によっては、ある状態に制御するのは容易でも、他の状態へ制御するのは難しい、ということがあり得ます。これは、ある状態への遷移を制御することは、他の状態への遷移を制御することよりも大きな制御コストがかかると言い換えることができます。制御コストの評価をすることで、脳にどのような制御入力を行えば最も効率的な制御が実現できるのか、そして脳のどの部位が制御に重要な役割を果たすかということに対して理論的な予測を与えることができるようになります。
脳活動の制御コストを評価するため、先行研究では制御理論を用いたアプローチが提案され、多くの研究で応用されてきました(Gu et al, Nature Communications, 2015)。しかし、先行研究で用いられていた枠組みでは、脳活動はノイズを含み確率的に振る舞うという重要な特性が無視されていました。現実にはノイズがある脳活動に対して、ノイズを無視して制御コストを計算してしまうと、実際の制御コストが正しく推定できないことになります。
[研究内容]
そこで本研究では、確率的なモデルを用いることで、脳活動の確率的な振る舞いを無視することなく、制御コストを定量化する新しい枠組みを提案しました。本研究チームは先ず、確率的な神経システムにおける制御コストを制御のない過程と、目的の状態に制御される過程とが、確率分布としてどのくらい異なっているかによって定量化することを提案しました(図1、2)。2つの確率分布の距離はカルバック-ライブラーダイバージェンス(KLダイバージェンス、注3)という指標で定量化できます。KLダイバージェンスに基づいた制御コストを考えることで、脳活動の確率的な挙動を考慮に入れることが可能となります。ただし、目的の状態に制御される過程は多数存在するため、制御コストは様々な値を取り得ます。本研究チームは様々な制御過程の中でも最も制御のない過程に近いもの、つまりKLダイバージェンスが最小となる過程を最適な制御過程として考え、その際の最小の制御コスト及び最適な制御入力を求めました。
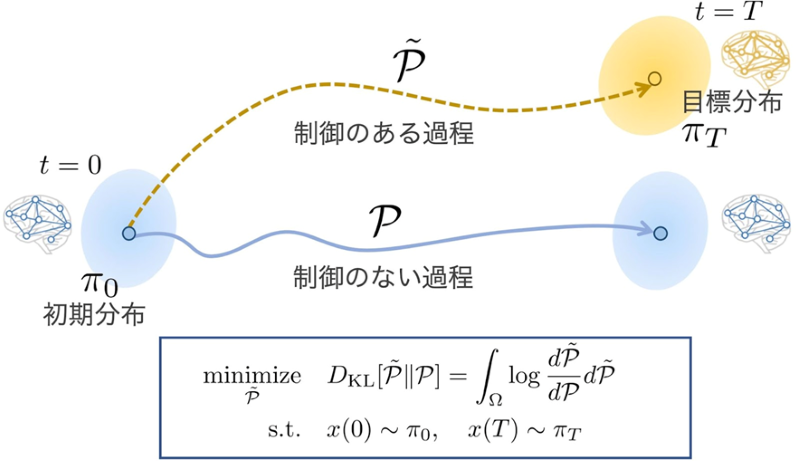
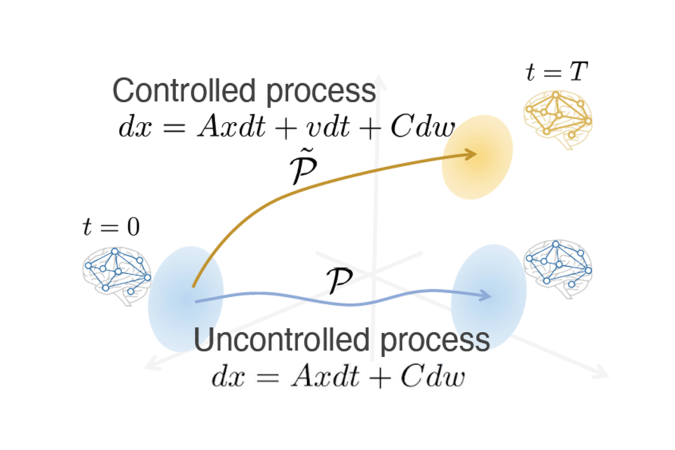
図1.本研究の概観。脳は時刻0のときにある確率分布0に従う状態にあるとします(左下青)。制御のないダイナミクス(青)では脳は確率分布π0 に居続けますが、制御されたダイナミクス(金色)では、脳は時刻Tである確率分布πT に遷移します。そして、このふたつの確率過程から決定される確率分布がどのくらい近いかを、確率分布の間の距離であるKLダイバージェンスで定量化します。このKLダイバージェンスの最小値を、青で表された状態から金で表された状態への遷移コストと定義します。
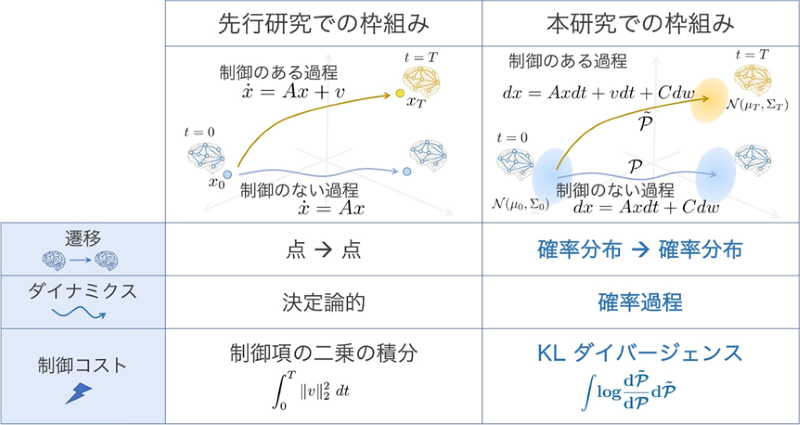
図2.先行研究と本研究の枠組みの違いの比較。先行研究(左)では脳のノイズを考慮することができておらず、脳の状態遷移は点から点、ダイナミクスは決定論的、制御コストは制御入力の2乗の積分としていました。本研究の枠組み(右)では、確率的なモデルを導入し、脳の状態遷移は確率分布から確率分布、ダイナミクスは確率過程、そして制御コストをKLダイバージェンスとして考えました。
本研究では、制御コストを数学的に扱いやすくするために、脳活動のダイナミクスを線形の確率微分方程式(注4)でモデル化しました。線形モデルを用いることで、最適な制御コストの解析解を得ることに成功しました。さらに、この最適なコストが「平均的な脳活動の変化を制御する項」と「脳部位間の相関の変化を制御する項(より正確には、共分散の変化を制御する項)」に分解できることを数学的に証明しました。
本研究チームは提案手法を、人間が様々な認知タスクを行っている際のfMRIデータ(Human Connectome Project; HCPで公開されているデータ、注5)に適用し、最適制御のコストを計算し、状態遷移の制御に重要な役割を果たす脳部位を特定しました。その結果、平均的な脳活動を制御するのには低次視覚野(注6)が重要なのに対し、脳部位間の相関(共分散)の制御には後帯状皮質(注7)と呼ばれる部位が重要であることがわかりました(図3)。
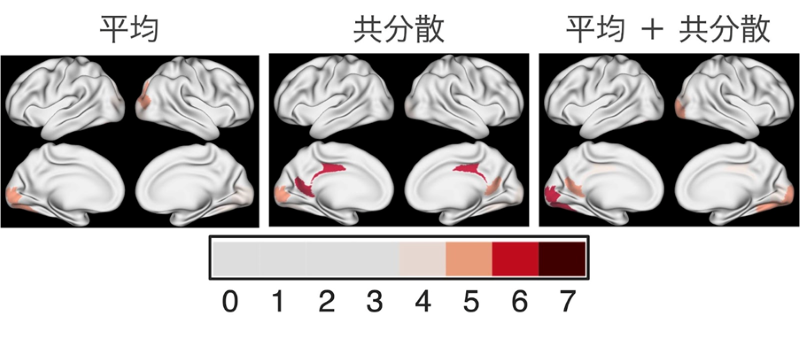
図3.安静状態から認知タスクへの状態遷移の制御に重要な脳領域を示しています。本研究での新しい枠組みのメリットの一つは、状態遷移における脳活動の平均、脳領域間の共分散を制御するのに重要な役割を果たす脳領域を特定できることです。左端と中央の図は、それぞれ平均と共分散の制御に寄与する領域を示しています。右端の図は、平均と共分散の和、つまり確率分布全体の制御に寄与している領域を示しています。図中の数字は、今回用いたHuman Connectome Projectに記録された7つの認知タスクのうち、何個のタスクで重要な脳領域として同定されたかを示しています。色が濃い領野が、異なる7つの認知タスクで共通して重要な脳領域と考えられます。
[社会的意義・今後の予定]
脳がある状態から別の状態に移り変わる際の制御コストを定量化することで、ある認知タスクを実行するときの認知的な負荷や、精神的疲労などを定量化することも可能になるかもしれません。また、どのような外部入力(磁気刺激・電気刺激など)を加えれば、最も効率良く目的の脳の状態に遷移させることが可能かといった臨床応用上の問題に対しても、理論的な予測を与えることができる可能性があります。
[謝辞]
本研究は、JSPS科研費(JP22J23428, JP18H02713, JP20H05712)、JST ムーンショット型研究開発事業JPMJMS2012、JST CREST JPMJCR1864の支援により実施されました。
プロジェクトマネージャーコメント
脳状態遷移コスト(制御コスト)から脳を見るという視点が斬新で、理論的な発展性のある研究となっている。また、数理的研究アプローチではあるが、そこから精神的疲労など定量的な評価を行える可能性を本研究が有している展望が、確かなサイエンスに基づいて人類が抱える課題を解決した未来を切り開いていくという点でまさにムーンショットらしい研究である。今回はfMRIを用いて実験したデータを活用して研究をしているが、今後は同じプロジェクトの中で研究されている非侵襲型BMIなど簡易的に計測した脳波を用いるアプローチなどで、さらにこの研究が発展していくことを期待している。 ムーンショット型研究開発事業 目標1 金井プロジェクト(身体的能力と知覚能力の拡張による身体の制約からの解放) プロジェクトマネージャー 金井 良太
論文情報
雑誌:The Journal of Neuroscience (1月11日)
論文タイトル:Optimal Control Costs of Brain State Transitions in Linear Stochastic Systems
著者:Shunsuke Kamiya, Genji Kawakita, Shuntaro Sasai, Jun Kitazono, Masafumi Oizumi*
DOI番号:10.1523/JNEUROSCI.1053-22.2022
用語説明
注1:脳のノイズ
脳の神経活動にはランダム性が常に存在する。例えば、ある神経細胞が同じ入力を受けたとしても、その反応には変動があることが知られている。他にも、大脳皮質の神経細胞は持続的自発発火活動と呼ばれるランダムな発火を示す。また、脳におけるノイズは人間の情報処理に重要な役割を果たす可能性も示唆されている 。
注2:機能的核磁気共鳴画像 (functional magnetic resonance imaging; fMRI)
ヒトの脳活動を測る方法の一つ。人間の頭部に磁場をかけ、ヘモグロビンとデオキシヘモグロビンの比を測定することで、血流量を間接的に推定する。脳活動が盛んな部位には血流が増えると考えられるので、脳活動の増加を見ることができる。
注3:カルバック-ライブラー(Kullback-Leibler)ダイバージェンス
確率分布P とQ が与えられたとき、それらがどれくらい異なるかを測る指標。確率変数Xが数の集合{a1,⋯,aN} のいずれかの値をとり、P とQ がX の確率分布とすると、P とQ の間のKLダイバージェンスD KL(P||Q) は
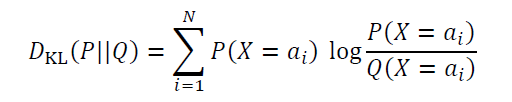
と定義される。ただしP(X=ai) で、確率分布P のもとでX がai となる確率を表す(Q(X=ai) についても同様)。D KL(P||Q) の値は常にゼロ以上となり、またゼロとなるのはP とQ が等しいときに限られるので、確率分布P とQ のKLダイバージェンスはふたつの確率分布間の「距離」と解釈できる。ただし、一般にD KL(P||Q) とD KL(Q||P) の値は異なるので、数学で扱われる「距離」ではないことに注意。
注4:線形確率微分方程式
先ず、確率微分方程式とは、通常の微分方程式に確率的な影響を表すノイズ項を加えたもの。ノイズ項はしばしばブラウン運動としてモデル化される。次の関係式で記述される。
dXt = f(X(t),t) dt + g(X(t),t)dBt.
なお、f ,g は適当な関数、Bt は標準ブラウン運動である。線形確率微分方程式は、上記の確率微分方程式の中で、f ,g がX(t) と線形な関係を満たすもの。
注5:Human Connectome Project(HCP)
米National Institute of Health主導で収集された、ヒトfMRIの大規模公開データベース。1000人程度の被験者で、安静時の脳活動、7種類の認知タスクを行っているときの脳活動のデータが記録されている。
注6:低次視覚野
網膜から入った視覚の情報が先ず処理される大脳皮質の脳部位。脳の最も背側(後頭部)に位置する。
注7:後帯状皮質
脳を内側からみたとき、右脳と左脳をつなぐ脳梁のすぐ上の領域のうち、背側の部分をいう。脳の各部位と解剖学的・機能的に接続していることが知られている。明確な役割は明らかになっていないが、多様な認知プロセスと関係し、人間の認知の制御を行う機能を果たすという説もある。

