ニュース
![]() 2023.07.14
2023.07.14
【研究成果】生き物の代謝系は様々だが、その応答は普遍的である ――代謝経済学による線形応答関係の発見――
2023年7月14日
東京大学
発表のポイント
- 生き物の代謝系の振る舞いは種や細胞によって様々であり、そこに普遍的な法則はないと思われていたが、あらゆる生き物の代謝系の振る舞いを記述できるシンプルな線形応答関係式を発見した。
- 経済学から着想を得た手法を新たに開発し、代謝系の環境変化に対する応答に着目することで、物理学において知られる線形応答関係と類似の法則を新規に導いた。
- 本研究で見出した線形応答関係式を用いることで、様々な代謝系の挙動の予測ができることから、代謝を対象とした薬剤の開発やバイオ産業における物質生産性能の向上への貢献などが期待される。
発表概要
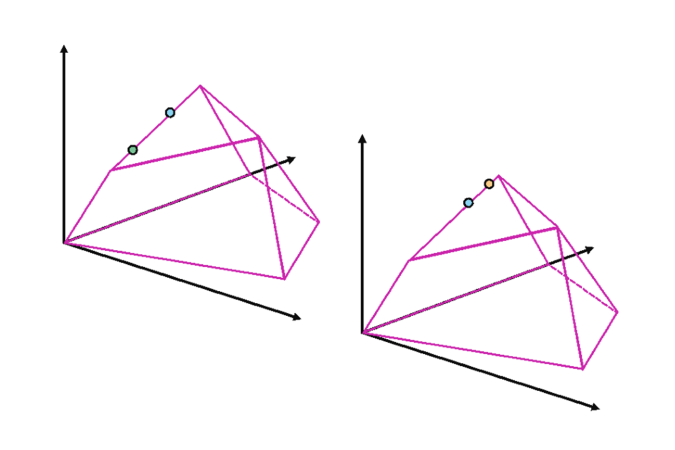
東京大学大学院総合文化研究科の山岸純平大学院生と畠山哲央助教は、ありとあらゆる生き物の代謝系において普遍的に成り立つ、環境変化への応答を記述する非常にシンプルな方程式を発見しました(図1)。

本研究は、細胞の代謝状態そのものは種や細胞によって様々であるにもかかわらず、代謝状態の環境変動や操作に対する応答に着目すれば、普遍的な法則が成り立つことを初めて示したものです。このような成果は、生物学における代謝系を対象として、経済学から着想を得た理論手法を新たに構築し、物理学において広く知られる線形応答理論(注1)との対応を論じるという学際的な研究によりもたらされました。
本研究で発見された線形応答関係式を用いることで、あらゆる細胞の代謝挙動について定量的な予測を与えることが可能です。これは、細胞の代謝状態を人間にとって望ましい方向へ操作・制御するための指針としても有用であり、代謝を対象とした新たな薬剤の開発や副作用の予測、バイオ燃料生産の効率向上など、基礎的な生命科学にとどまらず医学やバイオ産業まで、様々な分野に大きな貢献をもたらすと期待されます。
発表内容
〈研究の背景〉
代謝系とは、生き物が取り込んだ栄養をバイオマスやエネルギーに変換する生化学反応過程の総体のことで、生命の物理化学的基盤と言えます。細胞の代謝系の振る舞いを予測・理解することは、生物学の基礎研究として長年重要視されてきたのはもちろん、医学やバイオ産業・バイオ工学などの応用研究においても最も重要な課題のひとつです。
近年、システム生物学・代謝工学が発展する中で、何千ものパラメータを持つゲノムスケールの代謝モデルにおける最適解を数値シミュレーションすることで、現実の細胞の代謝状態を高い精度で予測できることがわかってきました。これは進化を経た細胞は、増殖率やバイオマス生産率などを最大化するよう、代謝状態やその遺伝子制御を最適化している、とみなせるためです。しかし、既存のシステム生物学・代謝工学における数値シミュレーションの予測値は代謝モデルの細部に強く依存しています。そのため、大規模代謝モデルを正確に作り込む必要があります。また、注目している生き物や細胞種ごとにそのような代謝モデルを構成することは容易ではありません。既存のアプローチのこのような特徴は、代謝系の振る舞いを定める原理の理解を阻むという基礎科学における困難だけでなく、医学やバイオ産業などへの応用における困難をももたらしています。
〈研究の内容〉
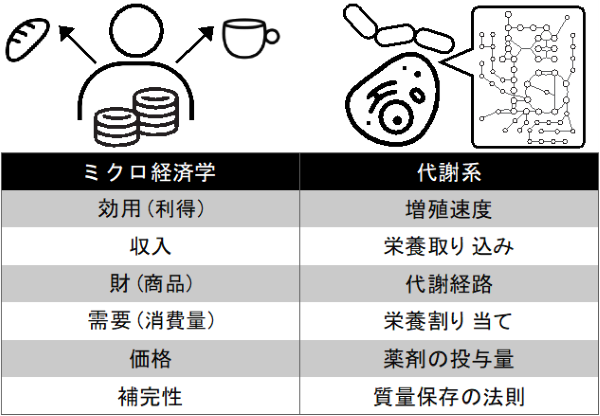
山岸と畠山は、上述の通り細胞内の代謝状態が最適化されていると見なせることを踏まえ、ミクロ経済学とのアナロジーに着目しました。ミクロ経済学は、「経済主体は利得(効用)を最大化するように振る舞う」という仮定にもとづき、消費者や企業の行動を説明・予測するための理論です。そのため、進化によって最適化された代謝系の振る舞いと、消費者の経済行動の間に厳密な数理対応を見出せます(図2)。この対応関係をもとにミクロ経済学における消費者行動の理論を適用することで、個々の代謝系の細部に依らない普遍的な理論を構築でき、実験に対しても新たな視点から定量的な関係式を与えることができました。
具体的には、ミクロ経済学におけるスルツキー方程式(注2)を用いることで、任意の細胞における任意の代謝経路について、栄養環境の変動に対する応答と、阻害剤投与などに対する応答とが常に比例するという「線形応答関係式」を理論的に導きました(図1)。この関係式は、質量保存則という物理化学的な制約の帰結としてあらゆる代謝系において成り立つべきもので、その背後には統計物理学における線形応答理論と同様の数理が潜んでいます。
この線形応答関係式を用いることで、個々の細胞が有する代謝反応ネットワークや「生き物が進化の過程でどのように最適化されているか」など、代謝系の細部についての情報なしに、栄養の量が変わった際にある代謝経路がどう応答するかという実験的に測定しやすい結果から、その代謝経路の薬剤応答についての定量的予測を与えることができます。実際、ゲノムスケールの代謝モデルの振る舞いを定量的に予測できることが、数値実験によって確認されました(図3)。また、興味深い振る舞いの例として、酵母やがん細胞において呼吸の阻害剤の投与がかえって呼吸を促進するという反直感的な現象(逆ワールブルク効果とも呼ばれる)を、説明・予測することも可能です。本研究で示された線形応答関係式からは、栄養の量の増加に伴って、ある代謝経路の流れが減少する場合には、一般にその代謝経路は阻害剤の投与によりかえって促進されるということが予測できます。
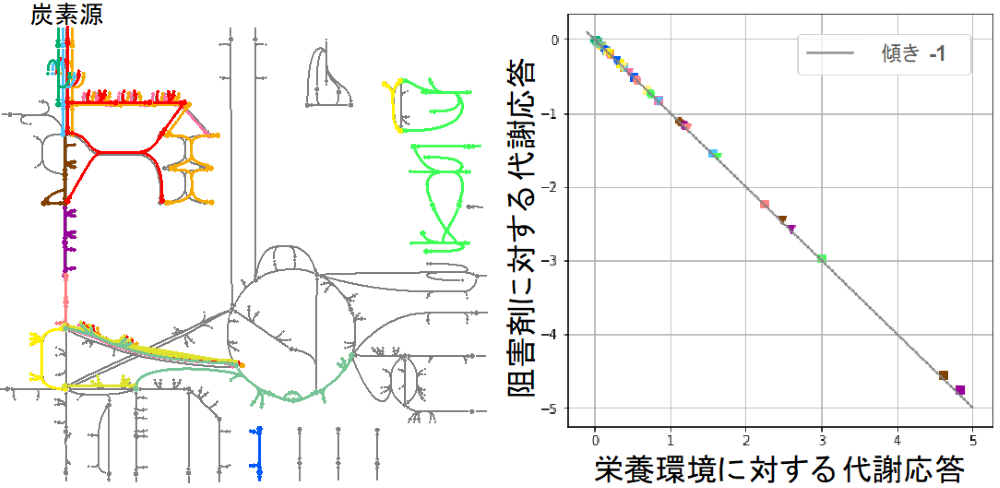
このような成果は、生物学の研究対象である代謝系の振る舞いについて理解するために、経済学から着想を得た理論手法を新たに構築し、物理学において広く知られる線形応答理論との関係を議論するという、非常に学際的なアプローチにより初めて得られたものと言えます。
〈今後の展望〉
本研究で見出された線形応答関係式は、あらゆる代謝系に対してその分子生物学的詳細についての事前知識なしに適用可能であるため、様々な細胞の代謝応答について定性的・定量的な予測をもたらすことが可能です。
このような理論は、細胞の代謝状態を人間が望む方向へ制御・操作するための定量的および定性的な指針としても有用であり、がん代謝などを対象とした新たな創薬ターゲットの提案および薬剤の副作用の予測、バイオ燃料の生産効率の向上など、生物学の基礎分野に限らず医学やバイオ産業・工学といった応用分野も含めた様々な分野に新たな道筋をもたらし、大きく貢献できると期待されます。
〈関連のプレスリリース〉
「「代謝経済学」によるがん細胞の代謝戦略の解明~代謝のワールブルク効果のメカニズムを経済学のギッフェン財との対応から解き明かす~」(2021/11/01)
https://www.u-tokyo.ac.jp/focus/ja/press/z0109_00023.html
発表者
東京大学 大学院総合文化研究科 広域科学専攻
山岸 純平(博士課程(日本学術振興会特別研究員))
畠山 哲央(助教)
論文情報
雑誌:Physical Review Letters(オンライン版:7月13日)
題名:Linear Response Theory of Evolved Metabolic Systems
著者:Jumpei F. Yamagishi, Tetsuhiro S. Hatakeyama
DOI:10.1103/PhysRevLett.131.028401
研究助成
本研究は、科研費「若手研究(課題番号:JP21K15048)」、「特別研究員奨励費(課題番号:JP21J22920)」および孫正義育英財団の支援により実施されました。
用語説明
(注1)線形応答理論
統計物理学において、熱平衡状態にある系が、外部の環境変化に対してどのように応答するかを記述する理論。
(注2)スルツキー方程式
ミクロ経済学の一分野である消費者行動の理論において、商品の消費量が、価格変化に対してどのように応答するのかと、所得の変化に対してどのように応答するのかの関係を記述する方程式。

