教養学部報
第645号 ![]()
ニューラルネットワークのエネルギー曲面上の滞留現象
今泉允聡
深層学習は非常に高い性能を発揮するデータ解析技術で、現代の人工知能の中核技術のひとつです。しかしその実用性の高さに比して、なぜ高い性能が出るのかという仕組みは未だ明らかになっておらず、今後の技術発展や安全な実用のために理論的な説明が求められています。特に重要度の高い未解決問題として、ニューラルネットワークの過学習の問題があります。深層学習で用いられるニューラルネットワークは、大量のパラメータを持つためその自由度が大変高いですが、訓練データに対して過剰に適合する"過学習"という現象が起こらないということが実験的に観察されています。これは大量のパラメータが過学習により精度を下げるという従来の理論と大きく矛盾しており、この問題を解消する理論が必要とされています。有力な仮説として、学習アルゴリズムの挙動が自由度を下げるという暗黙的正則化仮説が提唱されていますが、その具体的な形は未だに定説がありません。
我々の研究チームは、ニューラルネットワークがエネルギー曲面上で"滞留"という現象を起こすことを数学的に記述し、これが暗黙的な正則化となって深層学習が過学習を起こさないとする新理論を開発しました。ニューラルネットワークが学習を行う際には、確率的なアルゴリズムに基づいてエネルギー曲面上を遷移し、最適なパラメータを探索します。今回開発された理論では、このエネルギー曲面にある極小値の近傍が特定の構造を持つ際に、ニューラルネットワークがこの近傍に高確率で滞留し、これが暗黙的な正則化となって深層学習の過学習が起こらなくなることを証明しました(図1、2)。これまでの学説で、暗黙的正則化の具体的内容は数多く提案されてきましたが、有力な仮説に実験的な反例が出されるなど、有効な形は未だ定まっていませんでした。本研究によって、数学的に有効な形で暗黙的正則化の具体的な形が提唱されました。
深層学習は高い性能を発揮できるデータ解析手法ですが、その原理は未だ不明な点が多く、また計算コストの大きさや解釈性の低さといった実用上の問題点が多く残っています。本研究の成果は、深層学習の原理を解明するといった理論の試みに貢献し、人工知能のための新しい数学の構築につながるといった学術的な発展に加えて、ニューラルネットワーク設計や学習を効率化するアルゴリズムなどの工学的応用につながると考えられます。

図1 ニューラルネットワークのエネルギー曲面を次元圧縮したものの可視化(等高線)。
極小値(赤い丸)とその近傍(青い丸)が滞留を起こしうる領域を表す。
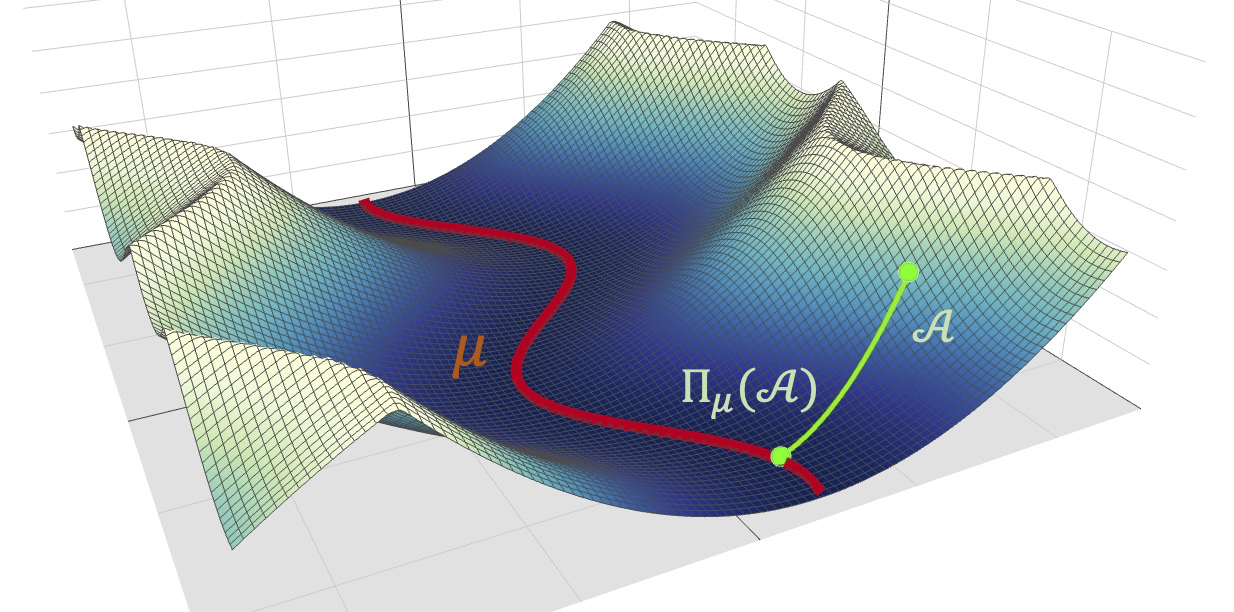
図2 エネルギー曲面中の極小値とその近傍のイメージ図。エネルギー曲面中の極小値の近傍で
局面が理想的な形状を持つ場合、その極小値は滞留を引き起こしうる。
(相関基礎科学/先進科学)
無断での転載、転用、複写を禁じます。

